Από τα πρώτα κρυπτογραφικά συστήματα μέχρι σύγχρονους κρυπτογραφικούς αλγορίθμους, το άρθρο αυτό περιέχει ό,τι χρειάζεται να ξέρεις για να γίνεις εξπέρ στην κρυπτογράφηση!
Η κρυπτογραφία είναι η επιστήμη που ασχολείται με τη μελέτη, την ανάπτυξη και τη χρήση τεχνικών κρυπτογράφησης και αποκρυπτογράφησης με σκοπό την απόκρυψη του περιεχομένου των μηνυμάτων.
Είναι δηλαδή το επιστημονικό πεδίο που μελετά τρόπους να μετασχηματίσει κανείς την πληροφορία με τέτοιο τρόπο, ώστε να είναι δύσκολη η ανάκτησή της χωρίς ειδική γνώση, κάτι που φαίνεται και από την ετυμολογία της λέξης (κρυπτογραφία < «κρυπτός» + «γράφω»).
Η κρυπτογραφία αποτελεί επιστημονικό κλάδο μεγάλης σημασίας, μιας και η συνεισφορά της κυρίως στους τομείς της ασφάλειας υπολογιστικών συστημάτων και επικοινωνιών είναι τεράστια. Γι’ αυτό, άλλωστε, συνιστά αντικείμενο μελέτης των εφαρμοσμένων μαθηματικών και της Πληροφορικής.
Ας δούμε, όμως, περισσότερες λεπτομέρειες γι’ αυτή.
Ιστορικά, η κρυπτογραφία χρησιμοποιήθηκε για το μετασχηματισμό ενός μηνύματος από μια κανονική μορφή σε ένα «ακατανόητο γρίφο», ώστε να αποφευχθεί η υποκλοπή του από τρίτους που πιθανόν έχουν πρόσβαση στο δίαυλο επικοινωνίας που χρησιμοποιείται.
Υπάρχουν δύο βασικές κατηγορίες κρυπτογράφησης: η κρυπτογράφηση που η επεξεργασία γίνεται πάνω στη γλωσσική δομή του μηνύματος (κυριαρχεί σε παλαιότερα κρυπτογραφικά συστήματα) και αυτή που αξιοποιεί τη θεωρία αριθμών και το αριθμητικό ισοδύναμο της έκφρασης (απαιτεί περαιτέρω εμβάθυνση σε διάφορους κλάδους των μαθηματικών όπως τα διακριτά μαθηματικά).
Η κρυπτογραφία χρησιμοποιείται ως τεχνική ήδη από την αρχαιότητα, όπως στη Μεσοποταμία το 1500 π.Χ. και στην Αρχαία Σπάρτη τον 5ο π.Χ. αιώνα με τις περίφημες σκυτάλες.
Ωστόσο, τα κρυπτογραφικά συστήματα που χρησιμοποιήθηκαν δεν είχαν την πολυπλοκότητα που χαρακτηρίζει τα σημερινά και έχει αποδειχθεί ότι μπορούν να αποκρυπτογραφηθούν πολύ εύκολα.
Παρόλα αυτά, όλες αυτές οι προσπάθειες δείχνουν την ανάγκη που υπήρχε από την αρχαιότητα κιόλας να παραμείνει ιδιωτική κάποια πληροφορία καθώς και την ευρηματικότητα των δημιουργών των συστημάτων αυτών.

Κρυπτεία σκυτάλη: Ένα από τα αρχαιότερα συστήματα κρυπτογράφησης. Στηριζόταν στην τεχνική της μετάθεσης χαρακτήρων με κλειδί την περιφέρεια της σκυτάλης. Το κείμενο αποτελούνταν από δύο μέρη που είχαν στην κατοχή τους τα εξουσιοδοτημένα μέλη και η (απο)κρυπτογράφηση γινόταν με καθορισμένο τρόπο όσον αφορά τον τρόπο τυλίγματος του κειμένου γύρω από τη σκυτάλη.
Όπως θα δούμε παρακάτω, οι πρώτες μέθοδοι κρυπτογράφησης χρησιμοποιούσαν δυο τρόπους αλλαγής του αρχικού μηνύματος: την αντικατάσταση και τον μετασχηματισμό.
Κατά τη διάρκεια του εικοστού αιώνα (ιδιαίτερα την περίοδο των δύο Παγκοσμίων Πολέμων) κατασκευάστηκαν αρκετές μηχανικές συσκευές που έκαναν αυτόματα αντικατάσταση.
Η πιο διάσημη από αυτές ήταν η συσκευή Enigma, η οποία χρησιμοποιήθηκε από τους Γερμανούς κατά τη διάρκεια του Β’ Παγκοσμίου Πολέμου για την αποστολή μυστικών μηνυμάτων στα στρατεύματα τους.
Ο κώδικας αναγνωρίστηκε από τους συμμάχους, αν και οι Γερμανοί άργησαν να αντιληφθούν ότι τα μυστικά τους αποκρυπτογραφούνταν.
Η τεχνική της αποκρυπτογράφησης ενός κρυπτογραφημένου μηνύματος δίχως να υπάρχει πρόσβαση στις λεπτομέρειες της μεθόδου κρυπτογράφησης ονομάζεται κρυπτανάλυση (ή διάσπαση κωδικών), ενώ ως πρωτόκολλα κρυπτογράφησης χαρακτηρίζονται οι ανταλλαγές μηνυμάτων μεταξύ διαφορετικών μερών που προσπαθούν να πετύχουν ένα στόχο με ασφάλεια π.χ. τον ορισμό του κοινού κρυφού κλειδιού κτλ.
Οι στόχοι της κρυπτογραφίας συνοψίζονται στις εξής βασικές λειτουργίες:
- Εμπιστευτικότητα: Η προς μετάδοση πληροφορία πρέπει να είναι κρυφή προς όλους, εκτός από τα εξουσιοδοτημένα μέλη της επικοινωνίας (αποστολέας, παραλήπτης).
- Ακεραιότητα: Διασφάλιση ότι μόνο ο εξουσιοδοτημένος αποστολέας και ο αντίστοιχος παραλήπτης μπορούν να αλλοιώσουν την προς μετάδοση πληροφορία.
- Πιστοποίηση ταυτότητας: Επιβεβαίωση της ταυτότητας ενός χρήστη.
- Πιστοποίηση μηνύματος: Διασφάλιση της πηγής και του προορισμού της πληροφορίας.
- Μη απάρνηση: Τα εξουσιοδοτημένη μέλη της επικοινωνίας πρέπει να αναλαμβάνουν την ευθύνη κάθε ενέργειας που έχει πραγματοποιηθεί και να μην αρνηθούν καμία αργότερα.
Κρυπτοσυστήματα
Ένα κρυπτοσύστημα αποτελείται από πέντε βασικά χαρακτηριστικά (P,C,K,E,D):
- P: το σύνολο των αποδεκτών μη κρυπτογραφημένων συμβολοσειρών.
- C: το σύνολο των αποδεκτών κρυπτογραφημένων συμβολοσειρών.
- Κ: το σύνολο των κλειδιών που θεωρούμε.
- Ε: το σύνολο των συναρτήσεων κρυπτογράφησης (μία για κάθε κλειδί).
- D: το σύνολο των συναρτήσεων αποκρυπτογράφησης (ομοίως μία για κάθε κλειδί).
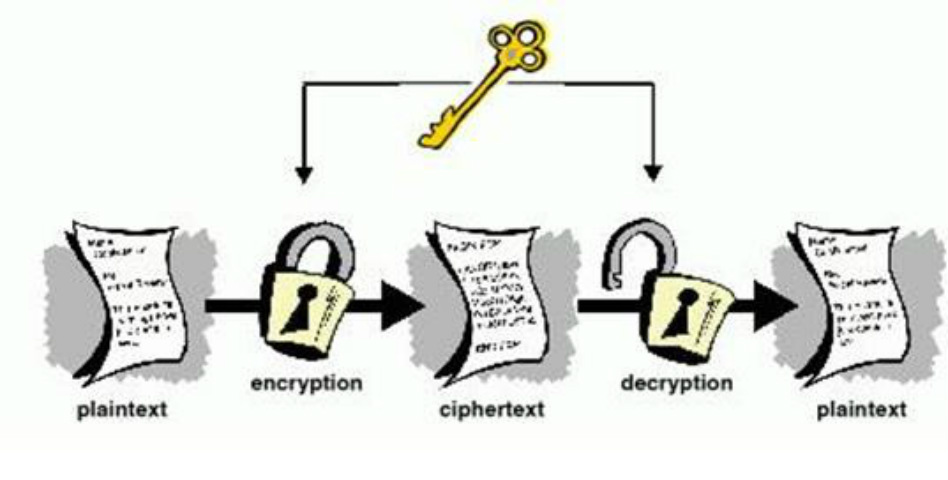
Έτσι, στη διαδικασία της κρυπτογράφησης, το αρχικό κείμενο (plaintext), που ανήκει στο σύνολο Ρ, μέσω ενός κρυπτογραφικού αλγορίθμου (cipher) μετασχηματίζεται σε μία νέα ακατανόητη μορφή, το κρυπτογραφημένο κείμενο ή ciphertext (συνήθως ο αλγόριθμος αποτελεί μια περίπλοκη μαθηματική συνάρτηση).
Το κλειδί είναι ένας αριθμός bit που δίνεται ως είσοδος στη συνάρτηση κρυπτογράφησης.
Η αντίστροφη διαδικασία συνιστά την αποκρυπτογράφηση.
Τα χαρακτηριστικά του κλειδιού διαφέρουν μεταξύ των διαφορετικών κρυπτοσυστημάτων.
Για να εξασφαλιστεί η αποτελεσματικότητα της κρυπτογράφησης, το κλειδί συνήθως είναι μυστικό και αποτελεί κοινή γνώση μόνο των εξουσιοδοτημένων μελών που καταλαμβάνουν τα δύο άκρα επικοινωνίας.
Ωστόσο, υπάρχουν και κρυπτοσυστήματα που στηρίζονται στην ύπαρξη δημόσιου και ιδιωτικού κλειδιού για την κρυπτογράφηση και την αποκρυπτογράφηση αντίστοιχα, τα οποία υπερκερνούν τον κίνδυνο υποκλοπής του κλειδιού κρυπτογράφησης, διότι οι δύο διαδικασίες χρησιμοποιούν διαφορετικά κλειδιά για την εκτέλεσή τους και το ιδιωτικό κλειδί είναι αρκετά δύσκολο να υποκλαπεί.
Επιπλέον, το μέγεθος ενός κλειδιού καθορίζει την ισχυρότητα της κρυπτογράφησης, αφού όσο μεγαλύτερος είναι ο αριθμός των bits τόσο πιο ανθεκτικό είναι συνήθως το σύστημα κρυπτογράφησης.
Είδη κρυπτογραφικών συστημάτων
> Κλασσικά κρυπτοσυστήματα
Στα κλασσικά κρυπτοσυστήματα εντάσσονται τα συστήματα αναδιάταξης και αντικατάστασης.
Τα συστήματα αυτά βασίζονται στην επεξεργασία των χαρακτήρων είτε με αναδιάταξη της σειράς εμφάνισης των χαρακτήρων είτε με αντικατάσταση κάποιου χαρακτήρα από κάποιον άλλον.
Οι τεχνικές αντικατάστασης είναι εκείνες στις οποίες τα γράμματα αντικαθίστανται από άλλα γράμματα ή σύμβολα ή αριθμούς. Υπάρχουν οι τεχνικές μονοαλφαβητικής αντικατάστασης, ομοφωνικής αντικατάστασης, πολυγραμματικής αντικατάστασης, πολυαλφαβητικής αντικατάστασης.
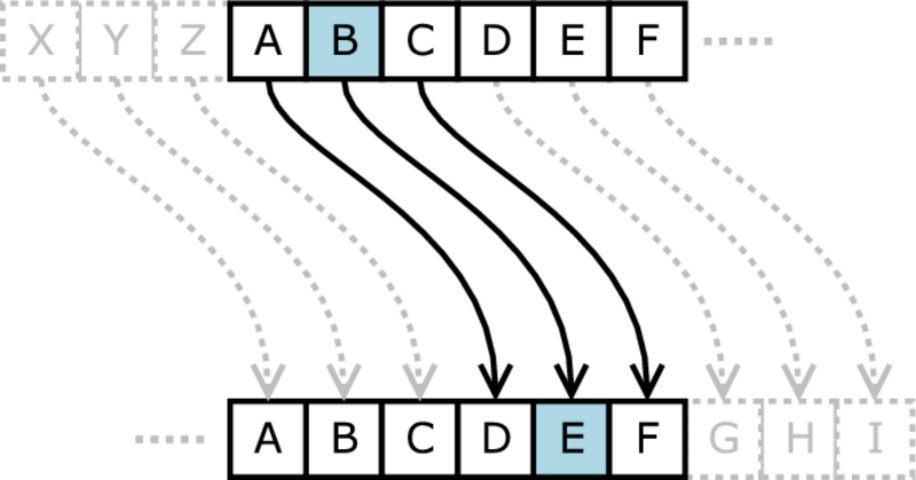
Ένα κρυπτοσύστημα αντικατάστασης είναι και αυτό που χρησιμοποίησε ο Ιούλιος Καίσαρας στην Αρχαία Ρώμη. Ο Καίσαρας έγραφε στους φίλους του αντικαθιστώντας τα γράμματα του κειμένου με τα γράμματα που βρίσκονται 3 θέσεις πιο μετά στο λατινικό αλφάβητο.
Στις μέρες μας, κάθε κρυπτοσύστημα που χρησιμοποιεί την τεχνική της ολίσθησης (δηλαδή την αντικατάσταση των γραμμάτων του αλφαβήτου με άλλα που βρίσκονται σε καθορισμένη θέση) ονομάζεται κρυπτοσύστημα αντικατάστασης του Καίσαρα.
Για παράδειγμα:
Θεωρήστε ότι έχουμε μηνύματα στο λατινικό αλφάβητο, όπου κάθε γράμμα αντιπροσωπεύεται από τον αντίστοιχο αύξοντα αριθμό μεταξύ 00-25. Αν θεωρήσουμε ως συνάρτηση κρυπτογράφησης το f(n) = (n+5) mod 26 (αντικατάσταση κάθε γράμματος από αυτό που βρίσκεται 5 θέσεις πιο μακριά) και ότι τα κενά και τα σημεία στίξης εμφανίζονται όπως είναι, η φράση “LET IT SNOW” γράφεται ως εξής:
| Πρωτότυπο κείμενο | L | E | T | I | T | S | N | O | W |
| Αριθμητικό ισοδύναμο | 11 | 04 | 19 | 08 | 19 | 18 | 13 | 14 | 22 |
| Αριθμητικό κωδικοποιημένο ισοδύναμο | 16 | 09 | 24 | 13 | 24 | 23 | 18 | 19 | 01 |
| Τελικό κείμενο | Q | J | Y | N | Y | X | S | T | B |
Προσέξτε ότι για το γράμμα W που αντιστοιχεί στο νούμερο 22 το ισοδύναμό του στην αριθμητική αυτή είναι το 01 επειδή η αντικατάσταση είναι κυκλική, δηλαδή μετά το τελευταίο γράμμα του αλφαβήτου επιστρέφουμε πάλι στην αρχή.
Έτσι, προκύπτει η έκφραση “QJYNYXSTB”.
Βασικό χαρακτηριστικό κάθε κρυπτοσυστήματος ολίσθησης είναι η αμφιμονοσήμαντη αντιστοιχία που πρέπει να διέπει τη συνάρτηση κρυπτογράφησης, δηλαδή κάθε χαρακτήρας πρέπει να αντιστοιχεί σε έναν και μόνο κρυπτογραφημένο χαρακτήρα, διαφορετικά ο παραλήπτης δεν θα μπορεί να αποκωδικοποιήσει ορθά το μήνυμα!
>Μονοαλφαβητικά κρυπτογραφήματα χαρακτήρων
Κάθε γράμμα του αλφαβήτου αντικαθίστανται από κάποιο άλλο γράμμα μέσα από τυχαία επιλογή. Παρόλο που είναι σχετικά εύκολη η διαδικασία της κρυπτογράφησης και αποκρυπτογράφησης των μηνυμάτων, το σύστημα αυτό είναι ευαίσθητο σε επιθέσεις υποκλοπής δεδομένων.
Αν επιθυμούμε να αποκρυπτογραφήσουμε ένα μήνυμα για το οποίο δε γνωρίζουμε την ακριβή τιμή ολίσθησης, δοκιμάζουμε όλες τις δυνατές ολισθήσεις (στο λατινικό αλφάβητο είναι 26). Όμοια λειτουργούμε και στην περίπτωση των μονοαλφαβητικών κρυπτοσυστημάτων.
Αν και πάλι οι προσπάθειες για την εύρεση του κλειδιού κρυπτογράφησης που απαιτούνται μέσα από επιθέσεις ωμής βίας είναι πάρα πολλές, προσπαθούμε να τη μαντέψουμε μέσα από την τεχνική της συχνότητας εμφάνισης των γραμμάτων μέσα στο κείμενο (λειτουργεί για μεγάλα κείμενα κυρίως).
Συγκεκριμένα, είναι γνωστό ότι στην αγγλική γλώσσα κάποιοι χαρακτήρες εμφανίζονται με μεγαλύτερη συχνότητα από κάποιους άλλους μέσα στα κείμενα.
Όσο πιο μεγάλο είναι ένα κείμενο τόσο πιο εύκολα μπορούμε να αντιστοιχίσουμε τις σχετικές συχνότητες εμφάνισης των γραμμάτων ενός κρυπτογραφημένου μηνύματος με τις αντίστοιχες της αγγλικής γλώσσας και να προκύψει ένα κείμενο που να βγάζει νόημα.
Αν η πρώτη αντιστοίχιση δεν δίνει κάποιο λογικό αποτέλεσμα συνεχίζουμε με τον επόμενο στη σειρά πιο συχνά εμφανιζόμενο χαρακτήρα μέχρι να προκύψει κάποιο κείμενο με νοηματική συνάφεια.
Για τις συχνότητες εμφάνισης των πιο συχνών χαρακτήρων του λατινικού αλφαβήτου ισχύουν(προσεγγιστικά): E : 13%, T : 9%, A : 8%, O : 8%, I : 7%, S : 7%, H : 6%, R : 6%.
>Αλγόριθμος κρυπτογράφησης Vigenere
Είναι μία μέθοδος κρυπτογράφησης σε αλφαβητικό κείμενο στο οποίο εφαρμόζονται διαφορετικοί αλγόριθμοι κρυπτογράφησης Καίσαρα με βάση τη θέση των γραμμάτων μιας λέξης ή φράσης κλειδί.
Είναι μια απλή μορφή της πολυαλφαβητικής υποκατάστασης. Τη μέθοδο αρχικά περιέγραψε ο Giovan Battista Bellaso το 1553.
Για παράδειγμα:
Έστω ότι η συμβολοσειρά κλειδί είναι η λέξη RED με αριθμητικά ισοδύναμα 17, 04, 03. Χωρίζω την προς κρυπτογράφηση λέξη σε τμήματα των 3 χαρακτήρων και αντιστοιχίζω κάθε χαρακτήρα του μπλοκ που προκύπτει με τον χαρακτήρα στην αντίστοιχη θέση στη λέξη- κλειδί.
Τότε για τη λέξη “ORANGE” το κρυπτογραφημένο μήνυμα που αντιστοιχεί μετά από ολίσθηση με τα μεταβλητά κλειδιά είναι:
|
Block που προκύπτουν |
ORA |
NGE |
||||
|
Πρωτότυποι Χαρακτήρες |
O |
R |
A |
N |
G |
E |
|
Αντίστοιχοι χαρακτήρες |
R |
E |
D |
R |
E |
D |
|
Αριθμητικό ισοδύναμο των πρωτότυπων χαρακτήρων |
14 |
17 |
00 |
13 |
06 |
04 |
|
Αριθμητικό ισοδύναμο κωδικοποιημένων χαρακτήρων |
05 |
21 |
03 |
04 |
10 |
07 |
|
Ισοδύναμοι χαρακτήρες |
F |
V |
D |
E |
K |
H |
>Κρυπτογραφήματα μετάθεσης
Τα κρυπτογραφήματα μετάθεσης ανήκουν στην κατηγορία των κρυπτογραφημάτων τμήματος, δηλαδή συστήματα αντικατάστασης τμημάτων γραμμάτων με άλλα τμήματα αντί να αντικαθιστούμε ξεχωριστά γράμματα με άλλα γράμματα, κάτι που καθιστά την αποκρυπτογράφηση αρκετά δυσκολότερη.
Σ’ ένα κρυπτογράφημα μετάθεσης, ως κλειδί χρησιμοποιούμε μία μετάθεση σ ενός συνόλου {1,2,..m} για κάποιο θετικό ακέραιο m, δηλαδή μια συνάρτηση 1-1 από το σύνολο αυτό προς το εαυτό του.
Για να κρυπτογραφήσουμε το μήνυμα, το διαμερίζουμε σε τμήματα μεγέθους m το καθένα (αν το πλήθος των γραμμάτων δεν επαρκεί ώστε να διαιρείται ακέραια από το m, προσθέτουμε τυχαία ορισμένα γράμματα στο τέλος για να συμπληρωθεί το τμήμα).
Κρυπτογραφούμε τα γράμματα κάθε τμήματος με βάση την μετάθεση σ και στη συνέχεια, η αποκρυπτογράφηση γίνεται με τη χρήση της αντίστροφης συνάρτησης σ-1.
Παράδειγμα:
Έστω ότι χρησιμοποιείται κρυπτογράφηση μετάθεσης με βάση τη μετάθεση: f(1) = 3, f(2) = 1, f(3) = 4, f(4) = 2.
Να κρυπτογραφηθεί το μήνυμα «HAPPY NEW YEAR» και να αποκρυπτογραφηθεί το κρυπτογραφημένο μήνυμα «ATSNCAALSSUIOICMGONTONTW».
•Χωρίζουμε το κείμενο σε τμήματα των 4 χαρακτήρων και αντικαθιστούμε τους χαρακτήρες με βάση τη συνάρτηση f. Δηλαδή, ο πρώτος χαρακτήρας μεταβαίνει στην 3η θέση, ο δεύτερος στην 1η, ο τρίτος στην 4η και ο τελευταίος στη 2η θέση.
|
Αρχικό κείμενο |
HAPP |
YNEW |
YEAR |
|
Κωδικοποιημένο |
APHP |
NWYE |
ERYA |
Ομοίως, για το κωδικοποιημένο μήνυμα, η τεχνική που ακολουθώ είναι η ίδια με μόνη διαφορά ότι αντιστοιχίζω τους χαρακτήρες με βάση την συνάρτηση f-1.
Επομένως, ο χαρακτήρας που βρίσκεται στην 3η θέση μεταβαίνει πρώτος, αυτός στην 1η θέση δεύτερος, από την 4η θέση τρίτος και από τη 2η θέση τέταρτος.
|
Αρχικό κείμενο |
ATSN |
CAAL |
SSUI |
OICM |
GONT |
ONTW |
|
Κωδικοποιημένο |
SANT |
ACLA |
USIS |
COMI |
NGTO |
TOWN |
Άρα, το « ATSNCAALSSUIOICMGONTONTW » είναι ισοδύναμο του «SANTA CLAUS IS COMING TO TOWN».
Bonus: Το κρυπτογράφημα του Κάμα-Σούτρα
Ναι, ξέρω το μυαλό όλων θα πάει στο πονηρό. Καμία σχέση, όμως. Όπως αναφέρεται στο βιβλίο του Κάμα Σούτρα μία από τις 64 τέχνες που πρέπει να γνωρίζει μία γυναίκα (συγκεκριμένα στο νο45) είναι η mlecchita-vikalpa, δηλαδή η τέχνη της μυστικής γραφής.
Η γνώση αυτή είναι απαραίτητη, ώστε να μπορεί η γυναίκα να καλύψει τα μυστικά των συνδέσμων της. Μία από τις συνιστώμενες τεχνικές περιλαμβάνει την τυχαία αντιστοίχιση γραμμάτων του αλφαβήτου και κατόπιν, την αντικατάσταση του αρχικού χαρακτήρα από το «σύντροφό» του. Για παράδειγμα:
Έστω τυχαία αντιστοίχιση των γραμμάτων του ελληνικού αλφαβήτου:
Α Κ Σ Τ Λ Γ Ω Ψ Ι Μ Η Ξ
Ν Δ Φ Β Ρ Χ Ε Ζ Ο Θ Π Υ
Η έκφραση «ΧΡΟΝΙΑ ΠΟΛΛΑ» κρυπτογραφείται ως: ΓΛΙΑΟΝΗΙΡΡΝ.
Στα κρυπτοσυστήματα αναδιάταξης εντάσσονται οι τεχνικές της μονοσταδιακής αναδιάταξης και της πολυσταδιακής αναδιάταξης.
Επίσης, στα κλασσικά εντάσσονται συνήθως τα γραμμικά κρυπτοσυστήματα, το αφινικό ή ομοπαραλληλικό κρυπτοσύστημα, το Hill κρυπτοσύστημα, τα συνδυαστικά κρυπτοσυστήματα (πχ κρυπτοσύστημα Playfair), το ADFGVX Κρυπτοσύστημα, οι “μηχανές με ρότορες”.
Όλα τα παραπάνω αποτελούν κρυπτοσυστήματα ιδιωτικού κλειδιού, δηλαδή η αποκρυπτογράφηση απαιτεί τη γνώση του κλειδιού κρυπτογράφησης για να επιτευχθεί.
Αν και είναι αρκετά ευαίσθητα στην κρυπτανάλυση, δεν ισχύει το ίδιο για όλα τα συστήματα ιδιωτικού κλειδιού.
Για παράδειγμα, το πρότυπο κρυπτογράφησης ιδιωτικού κλειδιού των Η.Π.Α., το λεγόμενο AES-Advanced Encryption Standard είναι αρκετά περίπλοκο και ανθεκτικό στην κρυπτανάλυση, γι’ αυτό χρησιμοποιείται ευρέως σε κυβερνητικές και εμπορικές εφαρμογές.
Ωστόσο απαιτεί τη δημιουργία ενός νέου κλειδιού για κάθε σύνοδο επικοινωνίας μεταξύ δύο μερών, κάτι που απαιτεί την ύπαρξη μιας γεννήτριας μεγάλης παραγωγής κλειδιών.
Μοντέρνα κρυπτοσυστήματα(Συμμετρικά και ασύμμετρα)
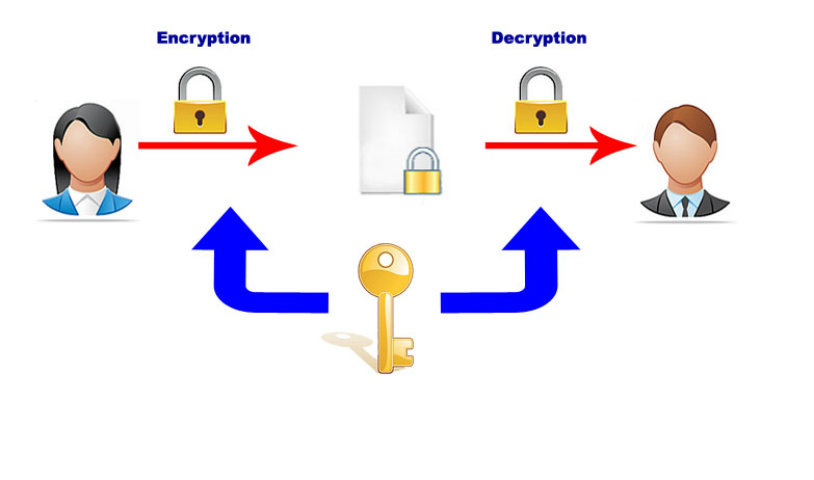
Ένα συμμετρικό κρυπτοσύστημα χρησιμοποιεί κατά τη διαδικασία της κρυπτογράφησης/αποκρυπτογράφησης ένα κοινό κλειδί.
Ένας τέτοιος αλγόριθμος είναι ασφαλής, εφόσον το κλειδί είναι απόλυτα μυστικό. Αυτό προϋποθέτει ότι το κλειδί είτε έχει ανταλλαχθεί μέσω ενός ασφαλούς διαύλου επικοινωνίας είτε μέσα από τη φυσική παρουσία των προσώπων.
Η κρυπτογράφηση συμμετρικού κλειδιού είναι πολύ αποδοτική όσον αφορά τους πόρους που απαιτούνται, ωστόσο έχει ένα βασικό πρόβλημα: το γεγονός ότι το κλειδί πρέπει να μεταφερθεί μέσω ενός ασφαλούς μέσου και θα μπορούσε να υποκλαπεί θέτοντας σε κίνδυνο την όλη διαδικασία.
Υπάρχουν διάφοροι αλγόριθμοι συμμετρικού κλειδιού που χρησιμοποιούνται σήμερα μεταξύ των οποίων συμπεριλαμβάνονται: Data Encryption Standard, CAST ,CMEA ,Triple-DES, IDEA, RC2, RC5 , RC6, Rijndael, RC4, MD2, MD4, MD5 κ.ά.
DES: Ο DES μετασχηματίζει μπλοκ χαρακτήρων αντί για απλούς χαρακτήρες. Χρησιμοποιεί κλειδί μεγέθους 56 bit και μπορεί να λειτουργήσει με διάφορους τρόπους ανάλογα με το επίπεδο ασφαλείας που απαιτείται. Ο DES είναι ένας αρκετά ισχυρός αλγόριθμος κρυπτογράφησης, ωστόσο μπορεί να σπάσει σχετικά εύκολα με έναν ειδικού σκοπού υπολογιστή(όπως αποδείχθηκε το 1999). Η πιστοποίηση του DES ανακλήθηκε το 1998 και αντικαταστάθηκε από έναν άλλο αλγόριθμο, τον 3DEA.
Τριπλό DES: Μια παραλλαγή του DES. Γίνεται με την εφαρμογή του DES τρείς φορές σε απλό κείμενο. Ο αλγόριθμος αυτός χρησιμοποιήθηκε από οικονομικούς οργανισμούς όπως τράπεζες ως μια πιο ασφαλής εναλλακτική του DES.
IDEA: Αυτός είναι ένας αλγόριθμος που αναπτύχθηκε στην Ελβετία και δημοσιοποιήθηκε το 1990. Χρησιμοποιεί ένα κλειδί μεγέθους 128 bit και δεν είναι πατενταρισμένος.
RC2: Αυτός είναι ένας αλγόριθμος που αναπτύχθηκε από τον Ronald Rivest. Μετασχηματίζει μπλοκ δεδομένων και χρησιμοποιεί ένα κλειδί μεγέθους από 1 εως 128 bits.
RC4: Αυτός είναι ένας αλγόριθμος που μετασχηματίζει το αρχικό κείμενο χαρακτήρα – χαρακτήρα. Αρχικά αποτελούσε εμπορικό μυστικό αλλά αργότερα δημοσιεύτηκε το σε μια ομάδα ειδήσεων το 1994. Μπορεί να χρησιμοποιήσει ένα κλειδί μεγέθους μεταξύ 1 και 2048 bits. Και αυτός ο αλγόριθμος, όπως ο RC2, αναπτύχθηκε από τον Ronald Rivest.

Ronald Rivest: Αμερικανός ερευνητής συστημάτων ασφαλείας. Σχεδίασε διάφορους κρυπτογραφικούς κώδικες μεταξύ των οποίων τους RC2, RC4, RC5 καθώς και τον περίφημο RSA μαζί με τον Adi Shamir and Len Adleman.
>Ασύμμετρα κρυπτοσυστήματα ή κρυπτοσυστήματα δημόσιου κλειδιού
Η Κρυπτογράφηση Δημόσιου Κλειδιού προέκυψε για να καλυφθεί η αδυναμία μεταφοράς κλειδιών που παρουσίαζαν τα συμμετρικά συστήματα.
Το βασικό χαρακτηριστικό της είναι ότι έχει δύο είδη κλειδιών, ένα δημόσιο και ένα ιδιωτικό.
Το δημόσιο κλειδί είναι γνωστό σε όλους και χρησιμοποιείται για την κρυπτογράφηση των μηνυμάτων των αποστολέων.
Η αποκρυπτογράφηση γίνεται με τη χρήση του ιδιωτικού κλειδιού του παραλήπτη, που είναι μυστικό. Η γνώση του δημόσιου κλειδιού ενός χρήστη δε βοηθά στην αποκρυπτογράφηση μηνυμάτων με αυτόν ως παραλήπτη.
Τα κλειδιά πρέπει δημιουργούνται σε ζευγάρια και πρέπει να είναι υπολογιστικά ανέφικτο να βρεθεί το ένα κλειδί από το άλλο.
Ο παραλήπτης ενός μηνύματος που χρησιμοποιεί κρυπτογράφηση δημοσίου κλειδιού χρησιμοποιεί τα δύο κλειδιά ως εξής:
- Δημοσιοποιεί το δημόσιο κλειδί του και οποιοσδήποτε θέλει να στείλει μήνυμα στο κάτοχο του κλειδιού χρησιμοποιεί το δημόσιο αυτό κλειδί για την κρυπτογράφηση.
- Η αποκρυπτογράφηση γίνεται από τον παραλήπτη εφαρμόζοντας κατάλληλο αλγόριθμο αποκρυπτογράφησης και χρησιμοποιώντας το ιδιωτικό κλειδί.
Αυτή η μέθοδος ανταποκρίνεται επαρκώς για μεγάλα κλειδιά και απομακρύνει το άγχος για την ασφαλή μετάδοση των κλειδιών.
Ωστόσο, η υπολογιστική ισχύς που απαιτείται για κρυπτογραφία δημόσιου κλειδιού είναι πολύ μεγαλύτερη από αυτή που χρειάζεται η κρυπτογραφία συμμετρικού κλειδιού.
Τα πιο γνωστά ασύμμετρα κρυπτογραφικά συστήματα είναι το RSA, το πρωτόκολλο Diffie-Hellman, το DSA, το πρότυπο ElGamal και η κρυπτογραφία ελλειπτικών καμπυλών.
Το RSA είναι το πιο γνωστό σύστημα σύστημα κρυπτογράφησης δημοσίου κλειδιού. Αναπτύχθηκε από τρεις καθηγητές στο MIT: τον Ronald Rivest, τον Adi Shamir και τον Leonard Adelman.
Το RSA δέχεται ως παραμέτρους 2 μεγάλους πρώτους αριθμούς και το δημόσιο κλειδί είναι το γινόμενο αυτών των αριθμών.
Η αποτελεσματικότητα αυτού του συστήματος έγκειται στο γεγονός ότι η παραγοντοποίηση ενός πολύ μεγάλου αριθμού σε γινόμενο πρώτων παραγόντων είναι πολύ δύσκολη και απαιτείται μεγάλη υπολογιστική ισχύς.
Αν βρεθεί η παραγοντοποίηση, τότε το σύστημα του δημοσίου κλειδιού μπορεί να σπάσει. Έχει βρεθεί ότι και το RSA παρουσιάζει έλλειμμα ασφάλειας, βέβαια, είναι περισσότερο ασφαλές από σχεδόν όλα τα κρυπτογραφικά συστήματα.
Εφαρμογές
Η εξέλιξη της κρυπτογραφίας έχει επιφέρει επανάσταση στον τεχνολογικό τομέα με αποτέλεσμα να χρησιμοποιείται ευρέως για διάφορους λειτουργικούς σκοπούς.
Μεταξύ αυτών συμπεριλαμβάνονται: η ασφάλεια συναλλαγών σε τράπεζες, κινητή και σταθερή τηλεφωνία, στρατιωτικά δίκτυα, ηλεκτρονικές επιχειρήσεις(ηλεκτρονικό εμπόριο), διαδίκτυο, έξυπνες κάρτες, VPN-ιδιωτικά δίκτυα, ασύρματα δίκτυα, τηλεδιασκέψεις, συναγερμοί κτλ.
Όπως φαίνεται, η σπουδαιότητα της επιστήμης της κρυπτογραφίας είναι τεράστια και η συμβολή της στην πρόοδο της ανθρωπότητας καθοριστική.
Όλοι μας μπορούμε να σχεδιάσουμε τον δικό μας κρυπτογραφικό αλγόριθμο, τηρώντας κάποιες βασικές αρχές (π.χ. αμφιμονοσήμαντη αντιστοιχία χαρακτήρων) για ιδιωτικούς σκοπούς που ενδεχομένως να μην επηρεάζονται υπερβολικά από το έλλειμμα ασφάλειας που διαπιστώνεται σε κάθε κρυπτοσύστημα.
Άλλοτε με περισσότερη εμβάθυνση και άλλοτε με πιο απλές αλλά αποτελεσματικές μεθόδους, η κρυπτογραφία είναι ένα εργαλείο για όλους μας, ακόμη και για καθαρά ψυχαγωγικούς λόγους.
Αν έχεις κι εσύ αυτή την τρέλα, τρέξε αμέσως να δημιουργήσεις το προσωπικό σου κρυπτογραφικό σύστημα! 😛